Understanding juggling Algorithm

The juggling algorithm is one of the solutions to array rotation problem, given below

given an array of integers, nums and a integer, k rotate the given array by k places
e.g nums : [1,2,3,4,5,6] & k = 4
ans [3,4,5,6,1,2]

the juggling algorithm that solves this is given as below

   void jugglingAlgo(int arr[], int d)
    {
        int n = arr.length;
        /* To handle if d >= n */
        d = d % n;
        int i, j, k, temp;
        int g_c_d = gcd(d, n);
        for (i = 0; i < g_c_d; i++) {
            temp = arr[i];
            j = i;
            while (true) {
                k = (j + d)%n;
                if (k == i)
                    break;
                arr[j] = arr[k];
                j = k;
            }
            arr[j] = temp;
        }
    }

the 1st question that pops up in the mind on seeing this is : why is there a gcd in array rotation problem?

Naive solution

A simple solution is to rotate the array 1 position at a time

[1,2,3,4,5,6] –> [6,1,2,3,4,5] –>[5,6,1,2,3,4] .. so on

a much better way would be to move the numbers directly to their final position.

Let’s juggle

Imagine this like playing a game

• you can pick 1 number in your hand
• you can replace any number with the number in your hand, the replaced number comes in the hand
• you can only have 1 number in your hand at any moment

[1,2,3,4,5,6]

so to solve the above array for k = 4 with minimum steps one would start moving the numbers like this

1: [_,2,3,4,5,6] : hand = 1 // pickup 1

2: [_,2,3,4,1,6] : hand = 5 // replace with 5

3: [_,2,5,4,1,6] : hand = 3 // replace with 3

4: [3,2,5,4,1,6] : hand = _ // put 3 in empty place

5: [3,_,5,4,1,6] : hand = 2 // pickup 2

6: [3,_,5,4,1,2] : hand = 6 // replace with 6

7: [3,_,5,6,1,2] : hand = 4 // replace with 4

8: [3,4,5,6,1,2] : hand = _ // put 4 in empty place

here we observe 2 things

• once we pick up a number, we keep on rotating/replacing the number to their final positions until we don’t have any number in hand
• if we don’t have any number in hand, and the array is not rotated completely, we pick up the number next to the number that we started with in the last iteration (step 5).

In the algorithm code that we saw at the beginning, the inner loop represents our 1st observation & the outer loop represents our 2nd observation.

Why gcd why

to understand how gcd comes into play we need to see how exact the inner loop works

For a moment instead of considering the array as circular, imagine the array as infinity long with array elements repeated

[1,2,3,4,5,6, 1,2,3,4,5,6, 1,2,3,…]

now if we start juggling in this array but just replacing numbers ahead i.e not moving back, the inner loop will iterate until we replace the same number that we started with (which would be a blank position)

[_,2,3,4, 5,6,1,2, 3,4,5,6, 1,2,3,…] : hand = 1

[_,2,3,4, 1,6,1,2, 3,4,5,6, 1,2,3,…] : hand = 5

[_,2,3,4, 1,6,1,2, 5,4,5,6, 1,2,3,…] : hand = 3

[_,2,3,4, 1,6,1,2, 5,4,5,6, 3,2,3,…] : hand = 1 / _

if we observe closely there are 2 intervals going on

• one with length = 6 i.e array length after which array is repeated
• second with length = 4 after which element is replaced

we keep replacing elements till we come to the element which we started with.i.e till the 2 intervals coincide

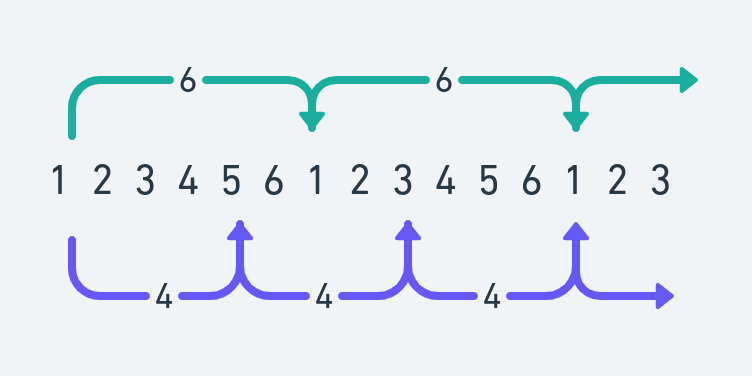
the 2 intervals will coincide after a distance of Least Common Multiple of (interval_1, interval_2) = LCM(n, d)

the number of element rotated in this distance of LCM(n,d) = LCM(n,d) / d

So the inner while loop will run ( LCM(n,d) / d ) times

Now the total number of elements to be rotated = n

so the number of iterations of the outer for loop should be

= n / (no. of iterations of inner loop)

= n / ( LCM(n, d) / d )

= n x d / ( LCM (n, d) )

= GCD(n, d)